Network Graphs & Solvers GUI Tutorial (DC)¶
The following guide provides step-by-step instructions to get started with using the Network Graphs & Solvers in Kinetica. This guide demonstrates some key graph concepts as well as how to create and solve a graph using the GAdmin graph GUI.
Prerequisites¶
D.C. Shape data file- Access to GAdmin
Data File¶
The tutorial makes use of the dc_shape dataset, which can be ingested from
the data file mentioned above.
To ingest the file using GAdmin:
- Navigate to GAdmin and login (
http://<kinetica-host>:8080/) - In the top menu, click
- In the top right corner, click Advanced CSV Import
- Click Select File and select the data file from your local directory
- Leave the default options and values for the rest of Step 1 and Step 2
- Under Step 3: Confirm, click Import CSV
The file will be validated and records will be inserted.
Key Information and Concepts¶
After the data file has been ingested into Kinetica, you should learn about the dataset and how it relates to the Network Graphs Solvers.
Data¶
The dc_shape dataset is a HERE dataset and is analogous to most road network
datasets you could find in that it includes columns for the type of road, the
average speed, the direction of the road, a WKT linestring for its geographic
location, a unique ID integer for the road, and more. The graph used in the
example is created with two columns from the dc_shape dataset:
shape-- a WKT linestring composed of points that make up various streets, roads, highways, alleyways, and footpaths throughout Washington, D.C.direction-- an integer column that conveys information about the directionality of the road, with forward meaning the direction in which the way is drawn in OSM and backward being the opposite direction:0-- a forward one-way road1-- a two-way road2-- a backward one-way road
You'll notice later that the shape column is also part of an inline
calculation for distance as weight during graph creation using
the ST_LENGTH and ST_NPOINTS
geospatial functions.
Graph Concepts¶
A graph typically comprises Nodes, Edges, Weights, Restrictions but only requires edges and weights. The graph created in this tutorial only uses edges and weights.
In this particular example, edges are logically mapped to sections of roadways and footpaths throughout the Washington, D.C., area. Each edge corresponds to a consecutive pair of points from each of the source LINESTRINGs, so a LINESTRING containing n points will have n-1 edges. Because the source graph is not created with nodes, implicit nodes are assigned at either end of each edge after graph creation.
For example, link ID 18350083 is a part of the Ward Circle roundabout, which
itself is part of Massachusetts Avenue Northwest near American University.
Selecting link ID 18350083 from the dc_shape table reveals the following WKT
linestring (the end of the linestring was removed for clarity):
LINESTRING (-77.08544159 38.93787003, -77.08544159 38.93793869, -77.08545685 38.9380188, -77.08548737 38.9381218, ...)
As noted above, each consecutive pair of coordinates will correspond to an edge in the graph, e.g.:
- Edge A -
LINESTRING(-77.08544159 38.93787003, -77.08544159 38.93793869) - Edge B -
LINESTRING(-77.08544159 38.93793869, -77.08545685 38.9380188) - Edge C -
LINESTRING(-77.08545685 38.9380188, -77.08548737 38.9381218)
Tip
After graph creation (and assuming the graph table was created), you can view each edge's details, including its respective WKT linestring, using WMS and clicking an edge:
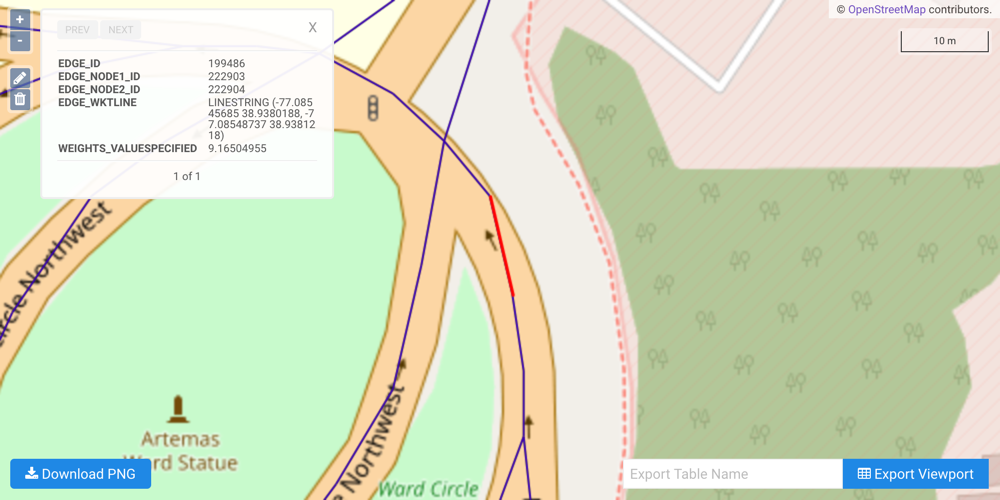
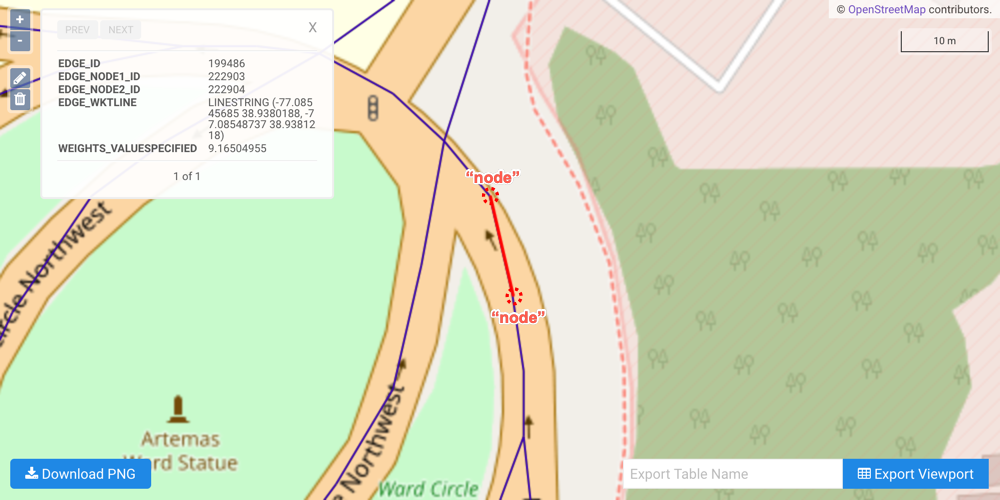
Each coordinate pair composing an edge is an implicit node:
Weights in this graph, as mentioned previously, are an abstract cost (distance, time, etc.) for travelling any roadway or footpath in the Washington, D.C., area. Weights are particularly important when solving a graph. There are two solver types presented in the tutorial below:
shortest_path-- Find the shortest path between two points on a graphmultiple_routing-- Find the quickest route between a source point and many destination points; also known as travelling salesman
Because there are no explicit nodes in the tutorial graph, source and destination point(s) must be selected from any of the edges comprising the Washington, D.C., road network. Otherwise, the graph will not be able to traverse to the point and will result in a null solution.
Tutorial via GUI¶
This tutorial is designed to be used with the GAdmin graph GUI. To access this GUI:
- Navigate to GAdmin and login (
http://<kinetica-host>:8080/) - In the top menu, click
All available graph actions are in the menu on the left side of GAdmin.
Create Graph¶
One graph is used for both graph solving examples in the tutorial:
dc_shape_graph, a graph based on the aforementioned dc_shape dataset.
To create the graph:
- From the graph GUI, in the left menu, click Create.
- Input
dc_shape_graphfor the Graph Name. - Select True under Directed Graph. The graph is directed because the roads in the dataset have directionality (one-way and two-way roads)
- Skip selecting a configuration for Nodes. The graph will have no explicitly defined nodes because the example relies on implicit nodes attached to the defined edges.
- For Edges:
- Click the configuration drop-down menu and select
EDGE_WKTLINE, EDGE_DIRECTION. - Click Add.
- Input
dc_shape.shapenext to as EDGE_WKTLINE. The edges will be derived from the WKT LINESTRINGs in this column. - Input
dc_shape.directionnext to as EDGE_DIRECTION. The edges' directionality will be derived from the integers in this column.
- Click the configuration drop-down menu and select
- For Weights:
- Click the configuration drop-down menu and select
WEIGHTS_EDGE_WKTLINE, WEIGHTS_EDGE_DIRECTION, WEIGHTS_VALUE_SPECIFIED. - Click Add.
- Input
dc_shape.shapenext to as WEIGHTS_EDGE_WKTLINE. This will match the weights to the edges by using the same WKTs. - Input
dc_shape.directionnext to WEIGHTS_EDGE_DIRECTION. This will match the weights to the edges' directionality. - Input
ST_Length(dc_shape.shape,1)/(ST_NPOINTS(dc_shape.shape)-1)next to as WEIGHTS_VALUESPECIFIED. The weights will be represented as distance, which is calculated as the length of the entireshapecolumn's LINESTRING (in meters) divided by the number of points in the LINESTRING minus 1
- Click the configuration drop-down menu and select
- Skip selecting a configuration for Restrictions. The graph will have no restrictions on any nodes or edges.
- For Options:
- Set the Merge Tolerance to
0.00001. This will merge nodes that are within one meter of each other. - Set Recreate to True. This will recreate the graph if it already exists.
- Set Enable Graph Draw to True and input
dc_shape_graph_tablefor the Graph Table. This will create a table containing the graph information in addition to creating the graph.
- Set the Merge Tolerance to
- Click Create New Graph. A WMS window will open, displaying the graph.
Solve the Graph (Shortest Path)¶
The following scenario has been designed to illustrate a shortest path solution:
You work near the White House, and after you get off work, you'd like to attend a baseball game at the nearby ballpark. What's the shortest path you could take to get to the ballpark?
Important
The source and destination points were selected from endpoints of
edges within the graph. The easiest way to review
the points that make up an edge is using the
WMS tool on the graph table
(dc_shape_graph_table).
| Source / Destination | Source | Destination |
| WKT | POINT(-77.03511810000001 38.89876175) |
POINT(-77.00585175000001 38.87462997) |
| Location Description | The corner of Madison Place Northwest and Pennsylvania Avenue Northwest | The corner of N Street Southeast and Southeast 1st street |
| WMS Location | 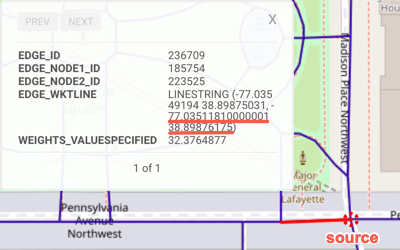
|
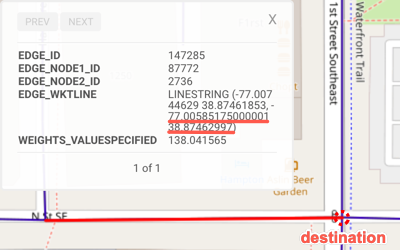
|
To solve the graph for shortest path:
From the graph GUI, in the left menu, click Solve.
Select
dc_shape_graphfrom the Graph Name drop-down menu.Skip selecting a configuration for Weights on Edges and Restrictions as there is no need for additional weights or restrictions.
Select
SHORTEST_PATHfrom the Solver Type drop-down menu.For Source Nodes, click the configuration drop-down, select
NODE_WKTPOINT, then click Add (there should be only one field). Input{'POINT(-77.03511810000001 38.89876175)'}next to as NODE_WKTPOINT.Note
Because the tutorial graph was created using WKT linestrings, the source and destination points are provided as WKT points.
For Destination Nodes, click the configuration drop-down, select
NODE_WKTPOINT, then click Add (there should be only one field). Input{'POINT(-77.0058078 38.8746344)'}next to as NODE_WKTPOINT.Input
dc_shape_graph_solved_shortest_pathfor the Solution Table.Leave the default Options.
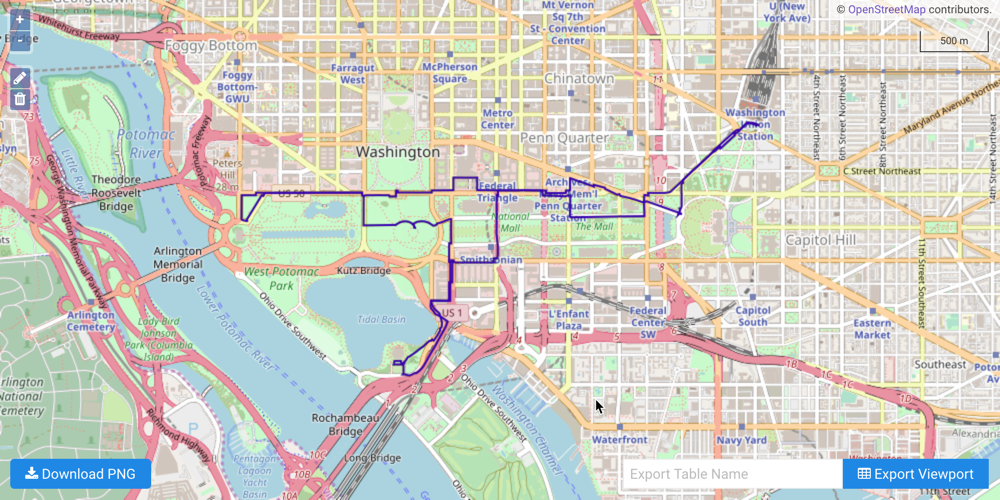
Click Solve Graph. A WMS window will open, display the solution:
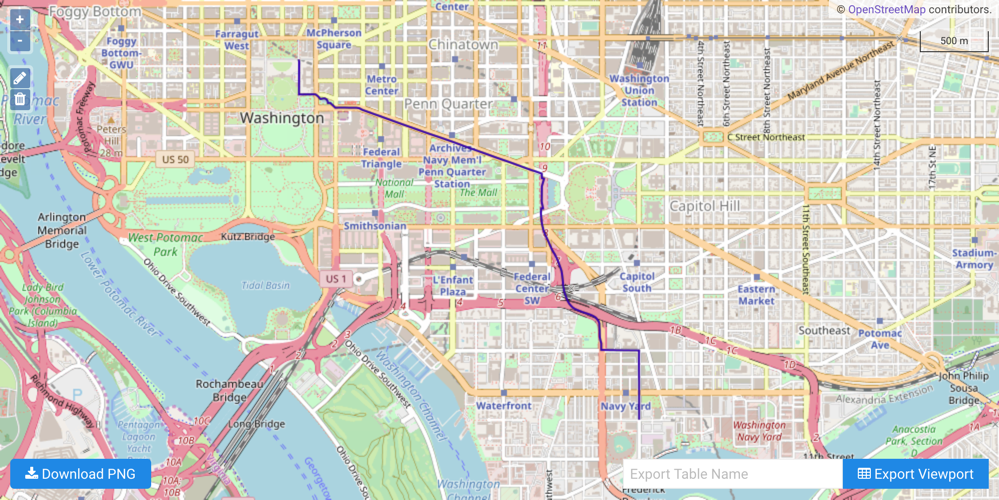
Solve the Graph (Multiple Routing)¶
The following scenario has been designed to illustrate a multiple routing solution:
You're currently taking the subway to Union Station to visit Washington D.C. for the day. You would like to see some of the most iconic monuments and buildings in Washington, D.C. before returning back to Union Station. Starting from Union Station, what's the quickest route between each stop before returning back to Union Station?
Important
The source and destination points were selected from endpoints of
edges within the graph. The easiest way to review
the points that make up an edge is using the
WMS tool on the graph table
(dc_shape_graph_table).
| Source / Destination | Source | Destination | Destination | Destination | Destination |
| WKT | POINT(-77.00576019 38.89677811) |
POINT(-77.03517151 38.8898201) |
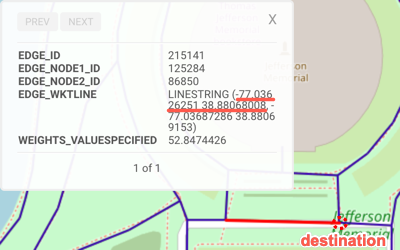
POINT(-77.03626251 38.88068008) |
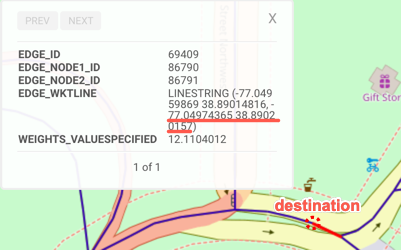
POINT(-77.04974365 38.89020157) |
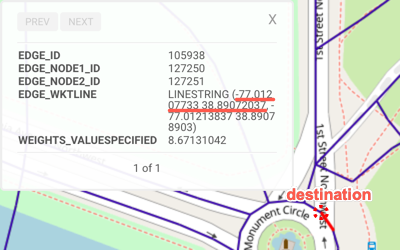
POINT(-77.01207733 38.89072037) |
| Location Description | Union Station | Near the Washington Monument | Near the Jefferson Memorial | Near the Lincoln Memorial | Near Capitol Hill |
| WMS Location | 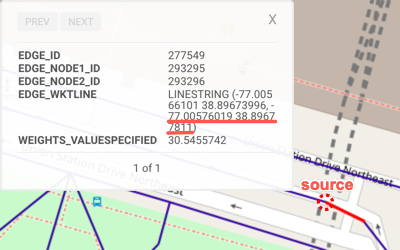
|
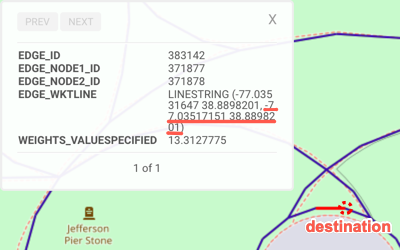
|
|
|
|
To solve the graph for shortest path:
From the graph GUI, in the left menu, click Solve.
Select
dc_shape_graphfrom the Graph Name drop-down menu.Skip selecting a configuration for Weights on Edges and Restrictions as there is no need for additional weights or restrictions.
Select
MULTIPLE_ROUTINGfrom the Solver Type drop-down menu.For Source Nodes, click the configuration drop-down, select
NODE_WKTPOINT, then click Add (there should be only one field). Input{'POINT(-77.00576019 38.89677811)'}next to as NODE_WKTPOINT.Note
Because the tutorial graph was created using WKT linestrings, the source and destination points are provided as WKT points.
For Destination Nodes, click the configuration drop-down, select
NODE_WKTPOINT, then click Add. Repeat until there are four destination fields. Input the following destination nodes:{'POINT(-77.03517151 38.8898201)'}{'POINT(-77.03626251 38.88068008)'}{'POINT(-77.04974365 38.89020157)'}{'POINT(-77.01207733 38.89072037)'}
Input
dc_shape_graph_solved_multiple_routingfor the Solution Table.Leave the default Options.
Click Solve Graph. A WMS window will open, display the solution: